Simple statistics of full data, like Mean ($\mu$) and Variance ($\sigma^2$), are generally required for critical tasks.

• Like centering the data to zero mean and unit variance ($\hat{x} = \frac{x-\mu}{\sigma}$)
  • This helps in making various dimensions in data scale invariant. For some functions, like $\hat{x}$ above, Mean and Variance, act as point estimators of data.

However estimating such point estimators from full data can be very slow for gigantic datasets, which may contain millions (or even billions) of samples.
Fortunately it is very common in Machine Learning to process data example-by-example or in mini-batches when either data is available in a sequential manner or in small batches (generally referred to as mini-batches). So we can leverage such method of processing to calculate our point estimators from running stream of data.

I have seen people using:

• Exponential Moving Average (EMA)
  • This method uses a full mini-batch at once to compute mini-batch (or sample) statistics.
  • Following are EMA Mean and Variance
    $\mu_{t} = \alpha*\mu_{t-N} + (1-\alpha)*sample\ mean_{t,t+N}$
    $\sigma_{t}^2 = \alpha*\sigma_{t-N}^2 + (1-\alpha)*sample\ variance_{t,t+N}$
    where:
    $\alpha \in [0,1)$
    • sample mean and variances are calculated from mini-batch of data containing N samples.
    • t is t’th calculated value
  • Pro:
    • Can be calculated fast
  • Con:
    • Requires a special parameter $\alpha$
    • Is a noisy point estimator of data, when mini-batch size is small
• Cumulative Moving Average (CMA)
  • Unlike EMA, this method uses each sample.
  • Finding CMA Mean is pretty straight forward. $\mu_{t} = \frac{(t-1)*\mu_{t-1} + x_{t}}{t}$
  • However CMA Variance is tricky. I derive a simple method below and show how accurate it is compared to EMA Variance.
    $\sigma_{t-1}^2 = \frac{\sum_{i=1}^{t-1} (x_{i}-\mu_{t-1})^2}{t-2}\\ \sigma_{t}^2 = \frac{\sum_{i=1}^{t} (x_{i}-\mu_{t})^2}{t-1}\\ \mu_{t}=\frac{\sum_{i=1}^{t} x_{i}}{t}\\ (t-1)*\sigma_{t}^2 - (t-2)*\sigma_{t-1}^2 = (x_{t}-\mu_{t})^2 + \sum_{i=1}^{t-1}((x_{i}-\mu_{t})^2 - (x_{i}-\mu_{t-1})^2)\\ = (x_{t}-\mu_{t})^2 + -2*(\mu_{t}-\mu_{t-1})\sum_{i=1}^{t-1}(x_{i}-\frac{\mu_{t}+\mu_{t-1}}{2})\\ = (x_{t}-\mu_{t})^2 + (t-1)*(\mu_{t}-\mu_{t-1})^2\\ So,\\ \sigma_{t}^2 = \frac{(t-2)*\sigma_{t-1}^2+(x_{t}-\mu_{t})^2}{t-1} + (\mu_{t}-\mu_{t-1})^2\\$
  • Pro:
    • Doesn’t require any special parameter
    • Is a solid point estimator (much less noisy)
  • Cons:
    • Is slower to calculate (could be made faster if implemented in a back-end library, based on C for example)

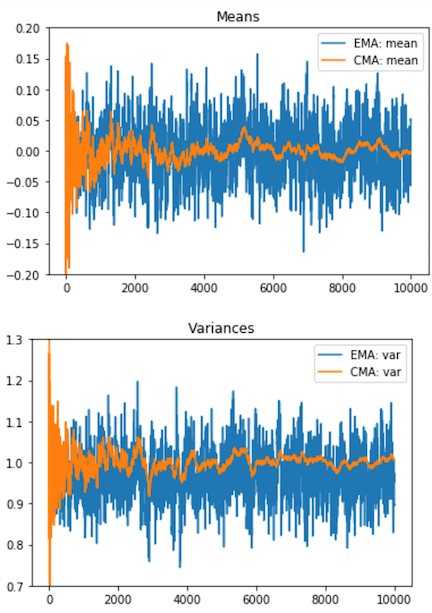
Following figures show comparison of Exponential and Cumulative Statistics of sampling done on Normal Distribution with Mean=0.0 and Variance=1.0
In each sampling event, 30 samples (=mini-batch size) were taken.
Then EMA statistics were calculate on whole mini-batch, while for CMA calculation was done on single samples as if they were fed sequentially.
$\alpha=0.9$ was used for EMA.

Conclusion

It is quite clear that EMA point estimators are quite noisy, where CMA estimators settle very close to actual distribution Mean (=0.0) and Variance (=1.0)